Verification of Bone Strength Pipeline in Abaqus
Final Year Dissertation Project
- In Affiliation with The Univeristy of Sheffield
- October 2022 - May 2023
Introduction
Performed a thorough literature review, assessing the impact of Osteoporosis (especially in elderly women), the use of computational (FEA) models to predict femur strength, and the format and conversion of VTK files to Abaqus INP files.
Successfully developed an Abaqus-based femur strength prediction Finite Element model, based on the Linear model obtained from existing literature, that achieves within 1% Minimum Femur Strength of the existing Ansys-based model for 15 loading orientations.
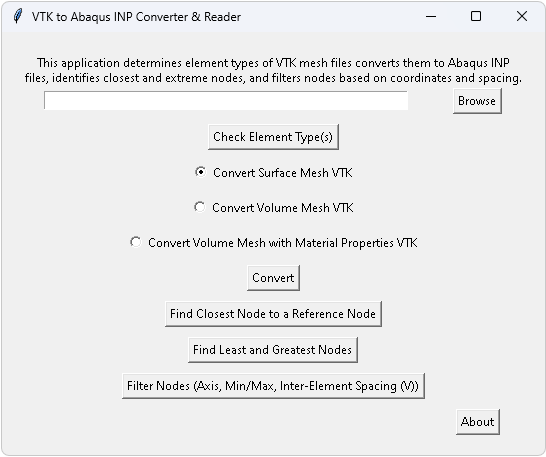
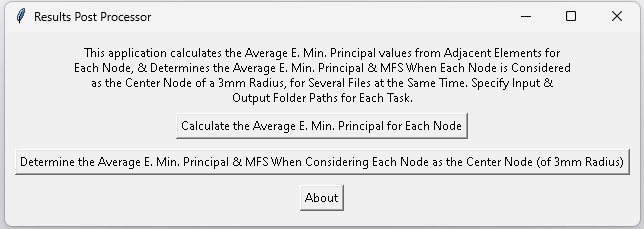
Developed the “VTK to Abaqus INP Converter and Reader” and “Results Post Processor” applications, using Python and relevant libraries, to automate and streamline the femur strength pre and post-processing to predict the MFS. Lays a firm foundation for future automation and integration with other applications.
The “VTK to Abaqus INP Converter and Reader” application: converts surface, volume, and volume mesh with material properties VTK files to corresponding Abaqus INP files, identifies the element type of input VTK file, and filters nodes based on various input parameters.
The “Results Post Processor” application: calculates the average minimum principal strain for each node from values yielded from adjacent elements and determines the average minimum principal strain and Minimum Femur Strength when considering each node as the center node of a 3mm radius using the linear force-strain relationship.
Brief:
Osteoporotic hip fractures are a major health concern, especially for women over 45, with side falls being the cause of 95% of such fractures. Numerous Finite-Element femur strength studies exist simulating a side-fall configuration for an older woman’s femur. This research project set out to verify an existing Ansys-based femur strength analysis in Abaqus, focusing on an 80-year-old woman’s femur under a side-fall condition. The project sought to ensure software enhancements, cross-platform accessibility, and alignment with industry requirements.
To achieve these goals, ASCII VTK files were converted to corresponding Abaqus INP files using Python scripts, and boundary conditions were applied. A Linear model was selected due to its extensive usage in previous studies and its ability to minimize potential discrepancies from other models. The primary objective was to ensure that the Abaqus-predicted Minimum Femur Strength (MFS) for the neutral orientation was within 1% of the Ansys-based counterpart.
The Abaqus-based femur strength model predicted the MFS as 2162.7N, which varied by only 0.4% from the Ansys-based counterpart in the neutral loading orientation. Fourteen other loading orientations achieved an average MFS of 2394N with an average percentage difference of nearly 0.1. However, thirteen loading orientations failed to reach the 1% MFS verification threshold, mainly due to inaccuracies in the boundary condition at the greater trochanter.
To streamline the femur strength analysis process, two Python-based applications, “VTK to Abaqus INP Converter and Reader” and “Results Post Processor“, were developed. These tools automated both the pre-processing and results post-processing, thus enabling efficient MFS predictions. The project’s findings lay a firm foundation for future work, with the potential for further automation or integration with other applications.
Aim:
Develop a femur strength analysis of an 80-year-old woman under side-fall conditions in Abaqus and verify based on the existing Ansys pipeline.
Objectives:
Covert an existing Ansys-based femur strength finite element analysis (FEA) pipeline for an 80- year-old woman’s femur under side-fall configuration to an Abaqus-based pipeline through the following process:
L1. Convert surface mesh (SM), volume mesh (VM), and volume mesh with material properties (VMMP) VTK files to Abaqus format INP files.
L2. Apply relative boundary and loading conditions on the respective node(s) for the chosen FE modelling approach.
Perform sanity checks for L1 and L2 to ensure the methods’ accuracy.
L3. Select an appropriate failure criterion and implement results post-processing methods to predict the MFS.
Ensure that the newly developed Abaqus-based model achieves an MFS within 1% of the existing Ansys-based model.
Hip fracture is a severe and costly injury affecting primarily older adults over 65, especially women. Approximately 76,000 hip fractures occur in the UK each year. It is typically a consequence of a weak bone structure (known as Osteoporosis) and a side fall and poses a greater risk to people of Asian or Caucasian descent. One in five men and one in three women over fifty will suffer fractures related to osteoporotic conditions.
Osteoporosis is a health condition that significantly weakens bones making them brittle and prone to fracture due to a decline in bone mass (the total amount of bone substance), hence becoming less dense and more vulnerable to fracture. The condition develops slowly over several years. Osteopenia is the stage before Osteoporosis, where the bone density obtained from bone density scans is lower than average for that age, gender, and ethnicity but not low enough to be classed as Osteoporosis. The condition develops slowly over several years and is usually identified upon sudden impacts such as side falls.
Osteoporosis is currently diagnosed by determining bone mineral density (BMD) using dual-energy X-ray (DXA) scans. The determined BMD value is compared with the average value for healthy females. Osteoporosis is defined when the BMD value equals or exceeds 2.5 standard deviations. Once diagnosed, the fracture risk is estimated using the BMD value and other parameters involving complex instruments. Although commonly used, this method (using the BMD value) predicts fractures at a rate of around 40% with a false positive of around 20%.
Computed tomography-based finite element methods have been increasingly used over the past four decades to simulate the mechanical behaviour of bones (predominantly adult bones). Given that 95% of Osteoporotic hip fractures are due to side falls, numerous femur strength FE studies exist that simulate an elderly woman’s femur under a side-fall configuration.
An existing Ansys model simulates the side-fall configuration of an 80-year-old woman’s femur. Converting the Ansys femur strength pipeline to an Abaqus-based pipeline offers several benefits. It ensures compatibility with software advancements and enhances accessibility for devices, users, and platforms where Ansys is not the primary FEA software. Developing and verifying an Abaqus-based femur strength pipeline will also enable SIMULIA to introduce software updates that align with industry requirements.